Seven Swans a Swimming Christmas Post

Where the Derivative Doesn't Exist
There are four functions/graphs where the derivative doesn't exist.

One of these is the absolute value function. The derivative doesn't exist at the corner.
f(x) = |x|

Another graph where the derivative doesn't exist is a cusp.

Piece-wise functions where there is a jump in the graph also don't have derivatives at the jump.

Rational functions lack a derivative at the asymptote.


Implicit Differentiation
Implicit differentiation is where you take the derivative of a function and you have multiple variables. When you find the derivative of each piece, you must multiply it by d(variable)/d(variable you are finding with regards to). Here is an example:

y² + x² = 3 Find dy/dx
2y(dy/dx) + 2x(dx/dx) = 0
2y(dy/dx) + 2x = 0
2y(dy/dx) = -2x
dy/dx = -x/y


The most important thing to remember while solving related rates problems is multiplying each piece by the correct d(variable)/d(variable). Otherwise, you will most likely not get the correct answer.

The Chain Rule and the Derivative

1) What is f' = 0?

f'(x) = 0 represents the maximum or minimum of f(x).

2) Identifying Where a Function Increases or Decreases

In order to identify where a function increases or decreases, you must first find the critical values of the function. This will give you the critical points which are possible maximums or minimums. Then you must plug in points before and after the critical points in the derivative. This will tell you if the points are negative or positive. You can use a number line to help visualize this. If the points go from negative to positive, then the function is increasing. If the points go from positive to negative, then the function is decreasing.

3) The Chain Rule

The chain rule is the process of finding the derivative of a composite function. Here are the steps to using the chain rule:
1) Take the derivative of the outside function.
2) Rewrite the interior function.
3) Multiply by the derivative of the inside.

Here is an example where we find the derivative and then the equation of the tangent line:

Find the tangent line of the function f(x) = (2x² + x)³ at the point x = -2

f'(x) = (2x² + x)³
        =  3(2x² + x)² • (4x + 1)
f'(x) = 3(2x² + x)² • (4x + 1)

f(-2) = (2(2)² + -2)³
        = (2(4) + -2)³
          = (8 + -2)³
        = (6)³
          = 216

slope = 3(2(-2)² + -2)² • (4(-2) + 1)
         = 3(6)² • (-7)
         = 3(36) • (-7)
         = 756
Our tangent line is:
y - 216 = 756(x + 2)
y - 216 = 756x + 1512
y = 756x + 1728

4) h(x) = f(g(x))
g(-4) = 5, g'(-4) = 2, and f'(5) = 20. Find h'(-4).

h'(x) = f'(g(x)) • g'(x)

h'(-4) = f'(g(-4)) • g'(-4)

h'(-4) = f'(5) • 2

h'(-4) = 20 • 2

h'(-4) = 40

Continuity and the Derivative

Continuous Functions
A function f(x) is continuous at x=a if:
1) The limit exists at x=a
2) f(a) exists (there is no hole/asymptote)
3) The limit at x=a is equivalent to f(a)

When a function isn't continuous:
          {x²+3, 0 < x
f(x) = {5, 0 = x
          {x+3, 0 > x

In order to check to see if a function is continuous, you must go through all three steps mentioned above. 

Step 1

We will see if the limit exists at x=a. We must look at the limit as x approaches the left and right of 0. The limit of the function as x approaches 0 from the left is 3. The limit of the function as x approaches 0 from the right is 3. This means that the limit exists.

Step 2

Next, we must make sure f(0) exists. By looking at the equation, we can see that f(x) = 5 when x = 0. This means that f(0) = 5 and f(a) exists. There isn't a hole or an asymptote.

Step 3

Finally, we must check to see if the limit at x=a is equivalent to f(a). Our limit as x approaches 0 is 3. However f(0) = 5. 5 doesn't equal 3. Therefore, the function isn't continuous.

Intermediate Value Theorem

If a function is continuous on a closed interval [a,b], and f(a) < N < f(b) then there is a < c < b such that f(x) = N.

We can use this theorem to tell if there is a solution on the interval [-2, 3] for the function f(x) = 2x² +3x - 5

 For this equation, f(-2) = -3 and f(3) = 22. Due to the fact that we know this function is continuous on the interval and the values are on opposite sides of the x-axis, we know there must be a solution in between them. We write this as: since f is continuous on [-2, 3], and f(-2) = -3 < 0 < 22 = f(3), then there exists c ∈[-2, 3] such that f(c) = 0.

Let's use this theorem on another function.

f(x) = 3x³ + 2 on the interval [-5, -1]

For this equation, f(-5) = -373 and f(-1) = -1. Due to the fact that both numbers are negative, we can't prove there is a solution on this interval. However, this doesn't mean there isn't one.

Derivatives

The derivative is basically the slope of a certain point in a function. There are two ways to find the derivative. One is by using the difference quotient and the other is by finding the derivative in terms of slope. We will find a linear derivative to demonstrate these concepts.

Difference Quotient

When we find the derivative by using the difference quotient, we use:

 lim   f(x+h)-f(x)

h→0        h

Find the derivative of f(x) = 3x + 5

3(x + h) + 5 - (3x + 5)

                h

3x + 3h + 5 -3x -5

             h

3x + 3h + 5 -3x -5

             h

3h

h

The derivative of this function is 3.

The Derivative in Terms of Slope

When we find the derivative in terms of slope, we use:

lim   f(x) - f(a)  at f(x) = a

x→a    x - a

Find the derivative of f(x) = 3x + 5 at f(x) = 2
3x + 5 - (3(2) + 5)
          x - 2

3x + 5 - 11
    x - 2

3x - 6
 x - 2

3(x - 2)
1(x - 2)

3(x - 2)
1(x - 2)

3
1

The derivative of this function is 3.

For me, the hardest thing about finding the derivative is foiling correctly while using the difference quotient.

Instantaneous Velocity and Average Velocity
Instantaneous velocity is the slope (or derivative) of an individual point. Average velocity is the derivative that can be used to find any point's slope for a particular function.

Limits

A limit is the behavior of a function as it approaches a certain point. This can be from the left or right.

In order to evaluate the limit, you should first plug in the number that the function is approaching. If you don't get a value and instead get undefined, you should use different methods depending on the type of function to solve for the limit. You should also try numbers on both sides of the number the function is approaching. This will verify if the limit is actually a true limit.

There are several ways to evaluate:
-Factor and cancel
-Rationalize using the conjugate (if there are square roots)
-Combine fractions

Factoring and Canceling

 lim     2x²-13x+15
x→5      x²+x-30

           2x²-10x-3x+15
             x²+6x-5x-30

           2x(x-5)-3(x-5)
           x(x+6)-5(x+6)

           (2x-3)(x-5)
            (x-5)(x+6)

           (2x-3)(x-5)
            (x-5)(x+6)      

            (2x-3)
             (x+6)

           (2(5)-3)
            (5+6)

           10-3
            11

lim     =    7
x→5        11

Rationalize using the Conjugate

lim      √(5x-6) -2
x→2      x²+x-6

           √(5x-6) -2  •√(5x-6) +2
             x²+x-6     •√(5x-6) +2

                        5x-10            
           (x²+x-6)(√(5x-6) +2)

                        5(x-2)             
           (x-2)(x+3)(√(5x-6) +2)

                        5             
          (x+3)(√(5x-6) +2)

                        5             
          (2+3)(√(5(2)-6) +2)

 lim      =  1
x→2        4

Combining Fractions
lim        1   _       1    
x→0     x²         x⁴+x²

             1( x²+1)    _       1    
             x²( x²+1)          x⁴+x²

                  x²+1    _       1    
              x⁴+x²          x⁴+x²

               x²    
            x⁴+x²         

                 x²       
           x²( x²+1) 

                  1   
            x²+1

lim      =
1
x→0


Piecewise Functions




In this graph of a piecewise function, you can tell where roots will and won't exist. Roots only exist when the graph approaches the same point from the left and the right. If the graph approaches different points when coming from different directions, the limit doesn't exist.

 For this graph, the limit as the function approaches -1 from the left is -1. The limit as the function approaches -1 from the right is also -1. This means -1 is a limit of the graph.

For this graph, the limit as the function approaches 2 from the left is 4. The limit as the function approaches 2 from the right is 3. Due to the fact that the limits are different, the limit does not exist.

Infinite Limits
Infinite limits are where the limit of a function is either ∞ or -∞.
An example of this type of function is:

lim      2
x→0   x²

You can enter any number close to 0 into the function and you will keep getting a large number. You can do this by approaching from the right or left. This means the limit as the function approaches 0 is ∞.

Polynomials and Triangles

f(x) = 4x³ - 4x² - 11x + 6

Here is our polynomial. A polynomial is an expression with at least two different algebraic terms.

Y-Intercept
When graphing a polynomial, you need to know the y-intercept. This is the point at which a graph crosses the y-axis (the vertical axis). To do this, you look for the constant. In our equation, 6 is the constant term. This means the y-intercept is 6, or (0,6). We need to write it as an ordered pair because it is a point on a graph.

Descartes
The next step in graphing if finding the number of possible real and imaginary solutions of the polynomial. The solutions are where the graph crosses the x-axis (the horizontal axis). We can already tell how many solutions the polynomial will have due to the largest exponent (the degree). The degree of our polynomial is 3. Therefore, we will have three solutions.

To find the possible positive solutions of the expression, we take the signs of all of the terms and see how many times the signs change.
The sign of 4 is +, the sign of -4 is -, the sign of -11 is -, and the sign of 6 is +.
+ - - +
The + changes to - and the - changes to +. This means there are either two or zero positive solutions. There might be zero positive solutions because there could be two imaginary solutions. Imaginary solutions only come in pairs. Therefore, when there are two or more solutions, you can take pairs out and say they could be imaginary.

To find the possible negative solutions of the expression, we take the expression and plug -x in for x. This might change some of the signs. Then we follow the same procedure as the one for positive solutions and count the number of changes.
f(x) = 4x³ - 4x² - 11x + 6 --> f(x) = -4x³ - 4x² + 11x + 6
The sign of -4 is -, the sign of -4 is -, the sign of 11 is +, and the sign of 6 is +.
- - + +
Only the one - changes to a +. This means there is only one possible negative solution.
Here is a chart showing the possible combinations of solutions:
+ | - | i 
2 | 1 | 0
0 | 1 | 2

Rational Root Test
The next step to graphing is to find all of the possible rational roots. In order to do this, we use the rational root test. To do this, we put all of the factors of the constant term (6 in our polynomial) over all of the factors of the leading coefficient (4 in our polynomial). This looks like this:
±1, 2, 3, 6
±1, 2 ,4
Then we divide and get all of the possible rational roots.
±1, 2, 3, 6,¹/₂, ³/₂, ¹/₄, ³/₄
These are our possible rational roots. There is a ± in front of them to show that our solutions could be positive or negative. This is because not all factors are positive.

Synthetic Division
Now, we need to find out which possible solutions are the right ones. We will do this through the use of synthetic division. This involves writing out all of the coefficients of the polynomial in a row, including the ones that don't show up. If there is a missing term, you put zero in for it. This is because a missing term could be 0x or 0. Then you put the possible rational root you want to test to the left of the coefficients. You then drop the leading coefficient down and multiply it by the possible root. Then you add the product to the next coefficient and drop down the sum. You take this sum and multiply it by the possible root and add the product to the next coefficient. You repeat this process until you get to the final coefficient. When you add the last product to the last coefficient, you should get zero. If the sum is zero, the possible root is one of the roots. If the sum isn't zero, then the possible root isn't a solution.
2 | 4 -4 -11 6
         8   8 -6  
     4  4  -3  0

¹/₂| 4  4  -3
          2    3 
      4  6    0

^-3/₂| 4  6
          -6   
       4  0
We now know all three of our solutions. x = 2, ¹/₂, and ^-3/₂
Our factors are (x - 2)(2x - 1)(2x + 3).

This solutions fit both Descartes and the rational root test because there are two positive roots and one negative root. All of the roots are also possible solutions according to the rational root test.

Behavior of the Graph
We know the beginning and ending behavior of the graph will be similar to that of a line because the degree of the polynomial is odd. If the degree was even, it would start and end like a parabola.
The graph will cross the x-axis at every root as opposed to bouncing off of it because each root has an odd multiplicity of one. If they had even multiplicities, the graph would hit the axis and bounce off.

Graph

By looking at the graph, we can see that all of our roots are there and it begins and ends like a line. The y-intercept is also 6. You can check this by plugging the equation into a graphing calculator and looking for the solutions in the table. You will find the roots in the x-value column and zero in the y-value column next to the roots.

Triangles
45-45-90 Triangle
The three angles of this triangle are 45°, 45°, and 90°.
The side lengths that corresponds to the two 45° angles is √2.
The side length that corresponds to the 90° angle (the hypotenuse) is 2.
The sin(45°) = ^√2/₂
The cos(45°) = ^√2/₂
The tan(45°) = 1

30-60-90 Triangle
The three angles of this triangle are 30°, 60°, and 90°.
The side length that corresponds to the 30° angle is 1.
The side length that corresponds to the 60° angle is √3.
The side length that corresponds to the 90° angle is 2.
The sin(30°) = ¹/₂
The cos(30°) = ^√3/₂
The tan(30°) = ^√3/₃

60-30-90 Triangle
The three angles of this triangle are 60°, 30°, and 90°.
The side length that corresponds to the 60° angle is √3.
The side length that corresponds to the 30° angle is 1.
The side length that corresponds to the 90° angle is 2.
The sin(60°) = ^√3/₂
The cos(60°) = ¹/₂
The tan(60°) = √3

First Assignment

The First Blog Assignment

1) The hardest topic in math so far was the Unit Circle in Math Analysis. This is because there was a lot of memorization of numbers involved.

2) The topic that has been the most fun in math so far were proofs in geometry. This is because they weren't very hard and it was sort of fun to try to figure out why a problem is correct.

3) My main goal in life is to become a lawyer in order to help others.

4) A school goal I have is to go to college and earn a JD. I can achieve this goal by getting an undergraduate degree, getting into a law school, and working hard to earn a JD.

5) A goal I have outside of school is to place well in the FBLA website design competition at districts. I can achieve my goal by planning my website ahead of time, working hard on the project, and practicing my presentation.

6) A function shows how an input and an output are related. Each input can only have one output. An example of a function is y=2x²-3

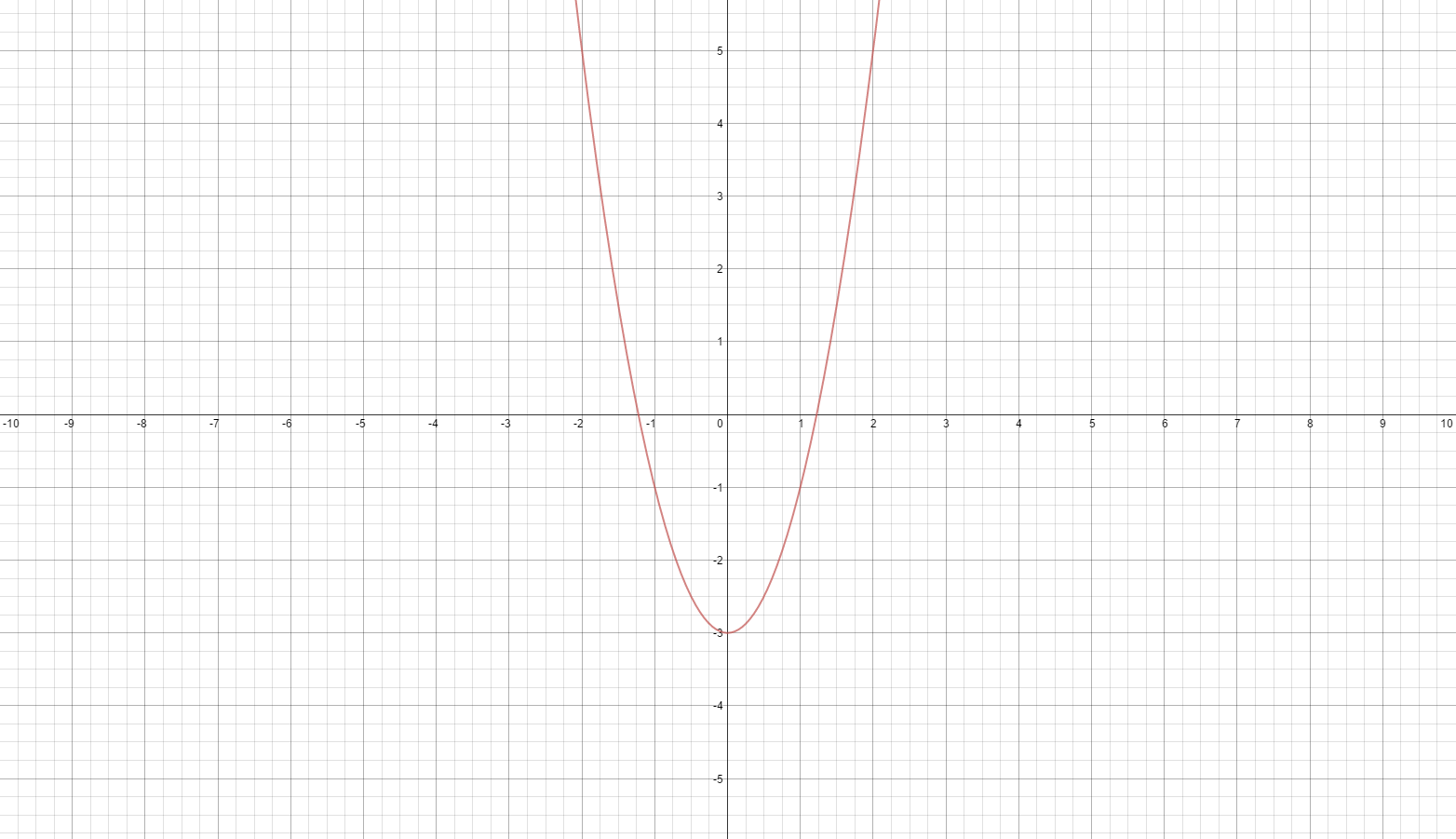 This graph shows the equation y=2x²-3